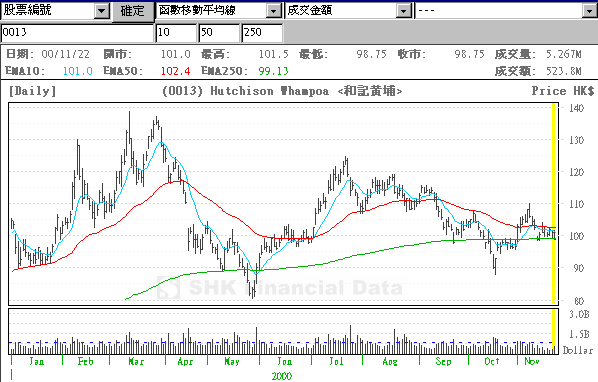
移動平均線是計算某段時間內的平均數值。 當計算移動平均值時，便需界定一段日數 (例如10日) 作為計算平均數值的基礎。

最常見的移動平均線日數為10日、50日及250日，但是你亦可以運用本公司的“智慧圖表系統”，將自己選擇的時段輸入圖表中間的空格內，你所需要的圖表便會即時顯示出來。

簡單移動平均數的計算方法是將一段時間內的股價加起，再除以這段時間的日數。 例如︰將某一股份最近14日的收市價相加後再除以14，計出來的數目便是最近14日的平均股價，其後一直向往後的日子推加新一日的收市價及剔除最前一日的收市價，再計出新的平均股價，如此類推，然後將每次計算出來的平均股價用線連上，便成為簡單移動平均線。

加權移動平均數的設計是將比重放在較近期的數據上，即是較近期的數據所佔的比例較大，而較遠期的數據佔的比例較少。 其計法是將每日收市價乘以一個權數，而這權數的數值決定於移動平均線的日數 (例如10日、20日、50日、100日或250日)。

以下是5日加權移動平均數的計算方法︰

為了減低簡單移動平均數的差距，技術分析員有時會運用函數移動平均數 (或函數加權移動平均數)。 在某程度上，函數移動平均數與加權移動平均數是頗為相似的，它們都是將比重放在較近期的數據上，而較遠期的數據所佔的比重則較少。 函數移動平均數所用的日數愈少，較近期的數據所佔的比重便愈大。 但要注意，函數移動平均數對較近期的數據的比重是較簡單移動平均數的比重為大，因此函數移動平均數會比簡單移動平均數對較近期的股價變動較為敏感。

X = 最新的函數移動平均數數值

C = 現貨價

P = 前一時段的函數移動平均數*

N = 函數移動平均數的時段

K = 平滑因子，其計法是 2 / (1 + N)

移動平均線代表投資者在某時段對市場普遍的期望。 例如︰如果股價是高於20日移動平均線，即表示投資者對這隻股份現時的期望 (即“現貨價”) 是高於他們對這股份20日的平均期望，因此投資者宜買入或增持這隻股份；反過來說，如果股價是低於20日移動平均線，即表示投資者對這隻股份現時的期望是低於其20日的平均期望，因此投資者宜沽出或減持這隻股份。 一般情況下，當股價升破移動平均線時，投資者宜買入該隻股份；而當股價跌穿移動平均線時，則宜沽出該隻股份。